Posición y desplazamiento

 

¿Qué significa la posición?

En física, nos encanta describir de forma precisa el movimiento de un objeto. En serio, los primeros capítulos de prácticamente cualquier libro de texto de física están dedicados a enseñarle a la gente cómo describir de forma precisa el movimiento, pues es muy importante para todo lo demás que hacemos en física.

Pero para describir el movimiento de un objeto, primero tenemos que describir su posición: en dónde está en cualquier momento en particular. De manera más precisa, necesitamos especificar su posición en relación a un marco de referencia conveniente. A menudo, la Tierra se usa como un marco de referencia, y usualmente describimos la posición de un objeto en relación a objetos estacionarios en ese marco de referencia. Por ejemplo, la posición de una profesora podría describirse en términos de dónde está en relación al pizarrón cercano (Figura 1). En otros casos, usamos marcos de referencia que no son estacionarios, sino que más bien están en movimiento en relación a la Tierra. Para describir la posición de una persona en un avión, por ejemplo, usamos el avión, no la Tierra, como el marco de referencia (Figura 2).

A menudo, se usa la variable $x$x para representar la posición horizontal. La variable $y$y suele usarse para representar la posición vertical.

[¿Qué hay acerca de z?]

¿Qué significa el desplazamiento?

Si un objeto se mueve en relación a un marco de referencia (por ejemplo, si una profesora se mueve a la derecha con respecto al pizarrón, o un pasajero se mueve hacia la parte trasera de un avión), entonces la posición del objeto cambia. A este cambio en la posición se le conoce como desplazamiento. La palabra desplazamiento implica que un objeto se movió, o se desplazó.

El desplazamiento se define como el cambio en la posición de un objeto. Se puede definir de manera matemática con la siguiente ecuación:

$\text{desplazamiento}=\Delta x=x_f-x_0$start text, d, e, s, p, l, a, z, a, m, i, e, n, t, o, end text, equals, delta, x, equals, x, start subscript, f, end subscript, minus, x, start subscript, 0, end subscript

$x_f$x, start subscript, f, end subscript se refiere al valor de la posición final.
$x_0$x, start subscript, 0, end subscript se refiere al valor de la posición inicial.
$\Delta x$delta, x es el símbolo que se usa para representar el desplazamiento.

[¿Qué significa el símbolo de triángulo?]

El desplazamiento es un vector. Esto significa que tiene tanto una dirección como una magnitud y se representa de manera visual como una flecha que apunta de la posición inicial a la posición final. Por ejemplo, considera a la profesora que camina en relación al pizarrón en la Figura 1.

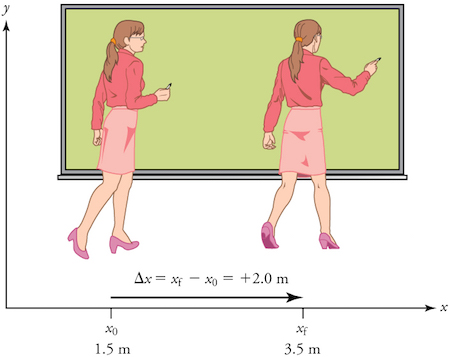
Figura 1: una profesora camina a la izquierda y a la derecha mientras da clases. El desplazamiento de $+2.0\text{ m}$plus, 2, point, 0, start text, space, m, end text de la profesora relativo al pizarrón está representado por una flecha que apunta a la derecha. (Crédito de la imagen: Openstax College Physics)

La posición inicial de la profesora es $x_0=1.5\text{ m}$x, start subscript, 0, end subscript, equals, 1, point, 5, start text, space, m, end text y su posición final es $x_f=3.5\text{ m}$x, start subscript, f, end subscript, equals, 3, point, 5, start text, space, m, end text. Entonces, su desplazamiento se puede encontrar como sigue: $\Delta x=x_f−x_0=3.5 \text{ m}−1.5\text{ m}=+2.0 \text{ m}$delta, x, equals, x, start subscript, f, end subscript, −, x, start subscript, 0, end subscript, equals, 3, point, 5, start text, space, m, end text, −, 1, point, 5, start text, space, m, end text, equals, plus, 2, point, 0, start text, space, m, end text. En este sistema de coordenadas, el movimiento hacia la derecha es positivo, mientras que el movimiento hacia la izquierda es negativo.

Ahora considera al pasajero que camina en relación al avión en la Figura 2.

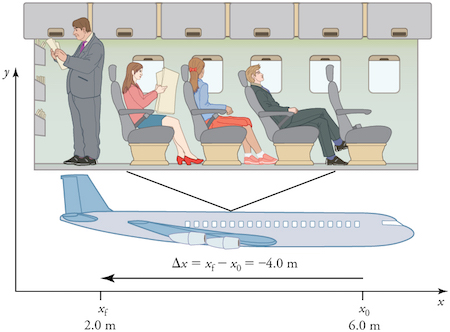
Figura 2: un pasajero se mueve de su asiento hacia la parte trasera del avión. El desplazamiento de $−4.0\text{ m}$−, 4, point, 0, start text, space, m, end text del pasajero en relación al avión se representa con una flecha dirigida hacia la parte trasera del avión. (Crédito de la imagen: Openstax College Physics)

La posición inicial del pasajero es $x_0=6.0\text{ m}$x, start subscript, 0, end subscript, equals, 6, point, 0, start text, space, m, end text y su posición final es $x_f=2.0\text{ m}$x, start subscript, f, end subscript, equals, 2, point, 0, start text, space, m, end text, por lo que su desplazamiento se puede encontrar como sigue: $\Delta x=x_f−x_0=2.0 \text{ m}−6.0\text{ m}=-4.0 \text{ m}$delta, x, equals, x, start subscript, f, end subscript, −, x, start subscript, 0, end subscript, equals, 2, point, 0, start text, space, m, end text, −, 6, point, 0, start text, space, m, end text, equals, minus, 4, point, 0, start text, space, m, end text. Su desplazamiento es negativo porque su movimiento es hacia la parte trasera del avión, o en la dirección negativa del eje x en nuestro sistema de coordenadas.

En el movimiento en una dimensión, la dirección se puede especificar con un signo positivo o negativo. Cuando comiences un problema, debes seleccionar cuál dirección es positiva (por lo general será hacia la derecha o hacia arriba), pero eres libre de elegir cualquier dirección como positiva.

¿Qué es la física?

¿Qué es la física?

Para ser honesto, es muy difícil definir exactamente qué es la física. Una de las razones es que la física sigue cambiando a medida que progresamos y hacemos descubrimientos. Las nuevas teorías no solo traen nuevas respuestas. También crean preguntas que incluso podrían no tener sentido cuando se observan desde las teorías previas de la física. Esto hace que sea emocionante e interesante, pero también fuerza a que los intentos por definirla se vuelvan generalizaciones acerca de lo que ha sido, en lugar de lo que puede ser en algún momento en el futuro.

Dicho eso, las definiciones son útiles. Así que si lo que quieres es una definición, eso es lo que obtendrás. En su mayoría, los físicos tratan de hacer lo siguiente:

1. Definir de manera precisa las cantidades medibles más fundamentales en el universo (por ejemplo velocidad, campo eléctrico, energía cinética). El esfuerzo para encontrar la descripción más fundamental del universo es una misión que históricamente siempre ha sido parte importante de la física, como se puede ver en la imagen de la historieta que se muestra a continuación.

   [Ocultar explicación.]

   Hay algunas cantidades medibles que no se consideran fundamentales, como la población de Irlanda o el valor de la bolsa de valores. Aún cuando esas cantidades son medibles, y teóricamente pueden describirse al usar una aplicación inconcebiblemente compleja de las leyes fundamentales de la física, típicamente no consideraríamos teorías sobre tales cosas como parte de la física. Es un poco impreciso decir en dónde se encuentra exactamente la línea entre lo que es fundamental y lo que no, además de que esta noción cambia con la historia.

   Una buena regla de oro es que si fueras a responder con las palabras "¿por qué?" una y otra vez sobre cualquier explicación que te estuviera dando tu profesor, la mejor y última respuesta que muy probablemente te podría dar sería una ley de la física, suponiendo que no te saque de su oficina antes de eso.
2. Encontrar relaciones entre esas cantidades fundamentales medibles (por ejemplo las leyes de Newton, la conservación de la energía, la relatividad especial). Estos patrones y correlaciones se expresan mediante palabras, ecuaciones, gráficas, tablas, diagramas, modelos y otros medios que nos permiten mostrar una relación de tal forma que nosotros, como humanos, podamos entender mejor y usar.

   [Ocultar explicación.]

   Lo creas o no, los principios, las gráficas, las leyes y las ecuaciones que se usan en la física no se crearon para hacernos más difícil explicar el universo. Al contrario, están ahí para facilitar su explicación y para ilustrar precisamente los patrones que encontramos en él. Esto le puede servir como pequeño consuelo a un estudiante de física que está luchando con un grupo de ecuaciones y definiciones aparentemente aleatorios y sin relación. Trata de recordar que debajo de todos esos símbolos matemáticos intimidantes y a veces extraños, a menudo hay una idea conceptual sencilla. Las matemáticas simplemente hacen posible formular una idea conceptual de una manera precisa y concreta.

Crédito de la imagen: Adventures Inside the Atom (Aventuras dentro de un átomo), 1948 General Electric, George Roussos (del dominio público)

Muy bien, reducir la física a solo dos cosas es sin duda una gran simplificación y pasa por alto algunos de los puntos más finos de qué hacen los físicos y cómo lo hacen. Pero la física se trata de describir un universo complejo con leyes simples, útiles y esclarecedoras. Así que tal vez intentar explicar la compleja actividad que realizan los físicos con una definición que sea simple y esclarecedora no es tan mala idea después de todo.

Estimados jóvenes DE SEGUNDO DE BACHILLERRATO
Ustedes van a encontrar en este espacio un video tutorial sobre la forma de expresar la concentración de las soluciones en unidades físicas. Observe el video y resuleva los 5 primeros ejercicios del archivo enviado a travé de la plataforma.

Cuida el medio ambiente

CIENCIA Y CIENTIFICO

SE PERSEVERANTE

              NANCY

TEORIA DE CUERDAS

LA TEORÍA DE CUERDAS

¿Qué es eso de la teoría de cuerdas?

 Publicado: Martes, 6 de Febrero de 2018

•  Universo
 
•  Física
 
•  Teoría de Cuerdas

Para entender este universo necesitamos de toda nuestra fuerza mental. Por eso disponemos de modelos que tratan de explicar lo que vemos de la mejor manera posible. Uno de ellos es el resonado modelo de cuerdas. Pero, ¿qué tiene de especial? ¿Por qué es tan importante? Esta teoría ha llevado de cabeza a los físicos de los últimos tiempos.

¿Cómo está formado el universo?

Este universo está regido por cuatro fuerzas fundamentalesque le dan forma y determinan sus leyes. Estas son la fuerza electromagnética, la fuerza "fuerte", la fuerza "débil" y la gravedad. Todas las partículas y subpartículas están sometidas a ellas, sin discusión.

"Las fuerzas fundamentales del universo son la electromagnética, la fuerza "fuerte", la fuerza "débil" y la gravedad"

Así, la concepción clásica que tenemos del universo comprende que las proteínas se forman a partir de átomos, y los átomos a partir de protones, neutrones y electrones. Más íntimamente tendremos partículas como quarks o leptones, que forman a estas unidades subatómicas; y aún más, en el límite de la física, están las partículas elementales que determinan cómo funcionan estas fuerzas fundamentales.

En lo más profundo del todo

Como decíamos, desde la materia que vemos, hasta las partes que forman a los átomos, todo está regido por las fuerzas universales. Pero, ¿y si profundizamos aún más, llegando hasta el límite de la física conocida? Puede ser, y solo es una hipótesis, que existiera algo aún más pequeño.

Esto no tendría forma de pelotita de masa, como normalmente imaginamos este tipo de elementos abstractos, al menos según la teoría de cuerdas. En vez de eso, estas pequeñas estructuras tendrían forma de una especie de filamentos o cuerdas, que vibran de determinada manera.

Según esta vibración, grosso modo, las cuerdas serían capaces de formar las distintas subpartículas (como un electrón o un bosón, por ejemplo). Hablamos de pequeñísimas cuerdas que miden 10^-35 metros, cercanas a lo que se conoce como "longitud de Planck", una escala de longitud por debajo de la cual se espera que el espacio deje de tener una geometría clásica. Esto significa que las cosas dejan de funcionar de la manera clásica.

A este nivel del universo, todo lo que conocemos, las dimensiones y todo lo demás, ya no funciona de la misma manera. Para que las cuerdas tengan sentido es imprescindible que existan más de las dimensiones a las que estamos acostumbrados. Y, aunque por el momento no hemos dado con esas dimensiones, algunos hechos matemáticos apuntan a su existencia.

¿Cómo funciona la teoría de cuerdas?

Según los cálculos físicos, las cuerdas se moverían en un espacio-tiempo distinto al ordinario, es decir, en un espacio llamado de tipo Kaluza-Klein, en el que a las cuatro dimensiones convencionales se añaden seis dimensiones compactadas de variedad de Calabi-Yau.

"Si un átomo midiera lo mismo que el sistema solar, las cuerdas tendrían el tamaño de una furgoneta"fuerte", la fuerza "débil" y la gravedad"

Por el momento, no hemos visto dichas dimensiones. Lo que, según los defensores de la teoría, se debería a que estas otras están compactadas y son inobservables en la práctica. Para hacer una analogía con una cuerda. Esta, desde lejos, es bidimensional. Pero según nos acercamos, la cuerda adquiere un grosor, y una profundidad, incluso una estructura. Las dimensiones serían como estas características.

Recordemos que hablamos de filamentos que son billones de veces más pequeños. Para hacernos una idea, si un átomo midiera lo mismo que el sistema solar, las cuerdas tendrían el tamaño de una furgoneta, más o menos. ¿Y para qué nos sirve una hipótesis que no podemos comprobar?

Explicar lo inexplicable

La respuesta a esta pregunta es, precisamente, para dar respuesta, valga la redundancia. La aparición de la teoría de cuerdas tiene ya unas décadas y trata de explicar el funcionamiento de las fuerzas de las que hablábamos y que rigen el universo. Esto se debe a que, por desgracia, los modelos actuales no son capaces de cumplir todo lo que esperamos de ellos a la hora de explicar la realidad.

Actualmente, la falta de pruebas de una subpartícula que explique la gravedad pone todos los modelos en un serio aprieto. Es lo que nos falta para desarrollar una "teoría del todo". La teoría de cuerdas es una aproximación que trata de profundizar más aún en los niveles físicos.

"Este es un marco teórico que se escapa por completo de nuestra capacidad para medirlo o tan siquiera comprenderlo por completo" ↜↝DIOS NO JUEGA A LOS DADOS....

Por el momento, no existe ninguna prueba práctica de que la teoría de cuerdas sea acertada, ni tampoco equivocada. Este, al fin y al cabo, es un mero marco teórico que trata de explicar qué ocurre, pero sin resultados tangibles. La única razón para optar por esta teoría en vez de cualquier otra es que el resto de modelos es inconsistente.

Puede que nunca lleguemos a comprobar algo tan efímero y profundo, ya que hablamos de un marco teórico que se escapa por completo de nuestra capacidad para medirlo o tan siquiera comprenderlo por completo. O puede que, quién lo sabe, algún día seamos capaces de comprobar por otras vías esta interesante y a la vez compleja hipótesis que sería ⇇⇇↶capaz de explicar el universo.